on
Formative Assessment in Math
1. Introduction
When discourses of education are reduced to school level, the educational process can be divided into three steps: first is inputs such as teachers, students, management rules, curriculums, and parental anxiety, second is classroom situation where actual interaction of teaching and learning takes place, and the last is outcomes such as students’ competency, teachers’ job satisfaction, and test results. While investing more resources to inputs and evaluating outputs are objective and visible, handling or promoting intercourse between teachers and students varies in every classroom situation, which are because the inputs and outputs are quantitative and classroom situations are qualitative. Thus, responsibilities for dealing with the experiences each student goes through in school lies all on to teachers. Therefore, in order for educational processes to be effective, it is required that further interests are put upon, and adequate investments and aids are provided to every vital interaction that occurs in classroom between students and teachers, or that between students. Assessing students’ development undertaken by teachers, and by students themselves that provide information to be used as feedback to modify teaching and learning activities is referred to as formative assessment(Black and William, 2005). In contrast to the widely spread concept of effective teaching as achieving high standards measured by test outcomes, formative assessment more focuses on continuous development of each students which is locus of learning. Marking high rank in PISA(Programme for International Student Assessment) among OECD(Organization for Economic Cooperation and Development) countries, Korea has become prominent in mathematics for attaining high national standard. However, though it inspired other countries for its noticeable interests in education, the results acquired from the PISA does not lead to the conclusion that students in Korea develop their Mathematical competency in their school environments. Since it is quite common for Korean students to take Math courses in advance to those of public school curriculum, students’ performance cannot be attributed alone to the learning which took place in school. As a result, it is required, in the context of Korea, to analyze the effect of formative assessment, and to investigate how it affects students’ growth.
1.1. Formative Assessment
The “diagnostic use of assessment to provide feedback to teachers and students over the course of instruction is called formative assessment”(Boston, 2002). By facilitating students’ metacognition from which they learn how to self-assess(Shepard, 2005), it is a way of raising students achievement(Black and William, 2005; Steadman, 1998; Shepard, 2005). According to Steadman(1998, p.26), The objects for making use of formative assessment are 1) to obtain feedback on the effectiveness of and student satisfaction with teaching and classroom activities, 2) to improve teaching, 3) to monitor students’ learning, 4) to improve students’ learning (in terms of retention or learning skills), 5) to improve communication and collaboration with students. However, it can have negative effect on students’ involvement in classroom when students perceive assessment, or feedback, as reproach from teacher or indication of their lack of ability(Black and William, 2005; Steadman, 1998).
1.2. Teacher-Student Relationship
One of the advantages which teachers take from employing formative assessment is improvement in teacher student relationship(Steadman, 1998). Furthermore, in order for formative assessment to be formative, it is required that teachers and students interact and co-operate(Shepard, 2005).
1.3. Self-Efficacy
According to Bandura’s social cognitive theory, self-efficacy refers to one’s judgments of confidence to perform academic tasks or succeed in academic activities. Teacher-student relationship affects students’ self-efficacy(Hughs and Chen, 2011), and it affects their mathematics performance(Pajares and Graham, 1999).
1.4. Research Questions
- Does formative assessment have direct positive effect on students’ mathematics performance?
- Are there indirect effects of Teacher-Student Relationship and Self-Efficacy on students’ mathematics performance?
2. Method
2.1. Participants
“PISA is the OECD’s Programme for International Student Assessment. PISA measures 15-year-olds’ ability to use their reading, mathematics and science knowledge and skills to meet real-life challenges”(PISA, 2020). The data is retrieved from PISA 2018 dataset. Test subject is mathematics. Among 6650 Korean students who responded questionnaires, 176 students who dealt with the same mathematics test items were selected.
2.2. Variables
2.2.1. Self-Efficacy
| CODE | Question |
|---|---|
| ST188Q01HA | I usually manage one way or another. |
| ST188Q02HA | I feel proud that I have accomplished things. |
| ST188Q03HA | I feel that I can handle many things at a time. |
| ST188Q06HA | My belief in myself gets me through hard times. |
| ST188Q07HA | When I’m in a difficult situation, I can usually find my way out of it. |
- scale
- 1 - Strongly disagree
- 2 - Disagree
- 3 - Agree
- 4 - Strongly agree
cronbach’s alpha is 0.7928646
2.2.2. Formative Assessment
| CODE | Question |
|---|---|
| ST102Q02TA | The teacher asks questions to check whether we have understood what was taught |
| ST102Q04TA | The teacher tells us what we have to learn. |
| ST104Q03NA | The teacher tells me in which areas I can still improve. |
| ST152Q05IA | The teacher encourages students to express their opinion about a text. |
| ST152Q08IA | The teacher poses questions that motivate students to participate actively. |
- scale
- 1 - Never or hardly ever
- 2 - Some lessons
- 3 - Most lessons
- 4 - Every lesson
cronbach’s alpha is 0.8412273
2.2.3. Teacher - Student Relationship
| CODE | Question |
|---|---|
| ST100Q01TA | The teacher shows an interest in every student’s learning. |
- scale
- 1 - Never or hardly ever
- 2 - Some lessons
- 3 - Most lessons
- 4 - Every lesson
| CODE | Question |
|---|---|
| ST211Q01HA | The teacher made me feel confident in my ability to do well in the course. |
| ST211Q02HA | The teacher listened to my view on how to do things. |
| ST211Q03HA | I felt that my teacher understood me. |
| ST213Q01HA | It was clear to me that the teacher liked teaching us. |
- scale
- 1 - Strongly disagree
- 2 - Disagree
- 3 - Agree
- 4 - Strongly agree
cronbach’s alpha is 0.8778682
2.2.4. Test Score
| CODE | Question |
|---|---|
| CM909Q01S | Speeding Fines - Q01 |
| CM909Q02S | Speeding Fines - Q02 |
| CM909Q03S | Speeding Fines - Q03 |
| CM949Q01S | Roof Truss Design - Q01 |
| CM949Q02S | Roof Truss Design - Q02 |
| DM949Q03C | Roof Truss Design - Q03 |
| CM00GQ01S | Advertising Column - Q01 |
| DM955Q01C | Migration - Q01 |
| DM955Q02C | Migration - Q02 |
| CM955Q03S | Migration - Q03 |
| DM998Q02C | Bike Rental - Q02 |
| CM998Q04S | Bike Rental - Q04 |
| CM905Q01S | Tennis balls - Q01 |
| DM905Q02C | Tennis balls - Q02 |
| CM919Q01S | Fan Merchandise - Q01 |
| CM919Q02S | Fan Merchandise - Q02 |
| CM954Q01S | Medicine doses - Q01 |
| DM954Q02C | Medicine doses - Q02 |
| CM954Q04S | Medicine doses - Q04 |
| CM943Q01S | Arches - Q01 |
| CM943Q02S | Arches - Q02 |
| DM953Q02C | Flu test - Q02 |
| CM953Q03S | Flu test - Q03 |
| DM953Q04C | Flu test - Q04 |
- Each question is scaled to have minimum value 0 and maximum value 1. Test score is sum of all questions listed above.
2.3. Analysis
2.3.1. Assumptions
- Multivariate Outliers
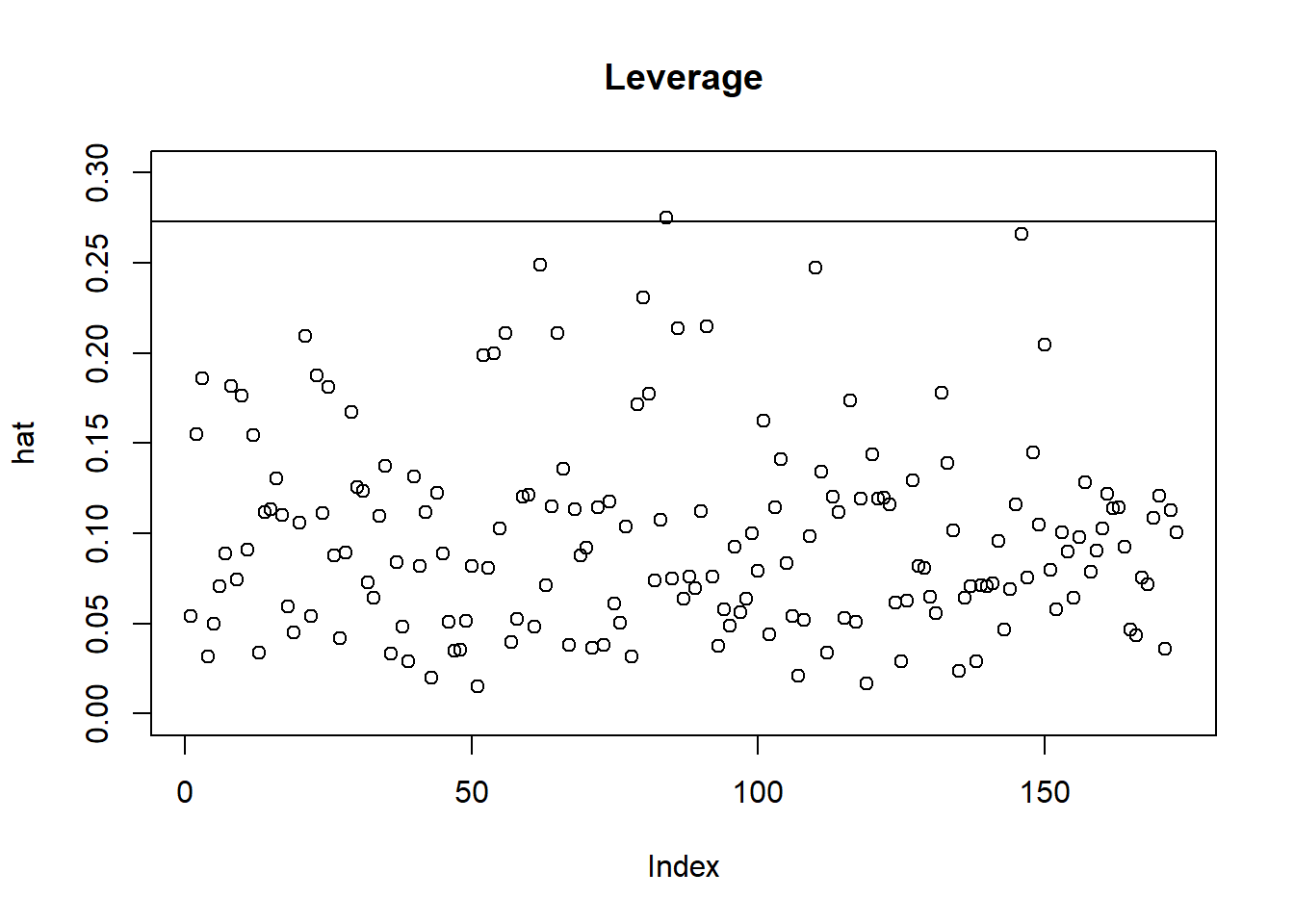
Although 84th and 85th students are detected as possible outliers, after further speculation, it is concluded that their responds are relevant. And thus, included in the dataset.
- Multicolinearity
| VIF | |
|---|---|
| ST188Q01HA | 1.665218 |
| ST188Q02HA | 1.494113 |
| ST188Q03HA | 1.703493 |
| ST188Q06HA | 2.487392 |
| ST188Q07HA | 2.115592 |
| ST102Q02TA | 2.201015 |
| ST102Q04TA | 2.193358 |
| ST104Q03NA | 2.247407 |
| ST152Q05IA | 2.582861 |
| ST152Q08IA | 2.857225 |
| ST100Q01TA | 2.234325 |
| ST211Q01HA | 3.172893 |
| ST211Q02HA | 3.155188 |
| ST211Q03HA | 3.528254 |
| ST213Q01HA | 2.117494 |
| Sum | 1.177941 |
Since all of the VIF values are less than 10, there is no multicolinearity detected.
2.3.2. Hypothesized Model
- Mediation model using structural equation modeling.
- Model
#add image
# blogdown:::insert_image_addin() 
3. Result
3.1. Effect of Formative Assessment on Test Score

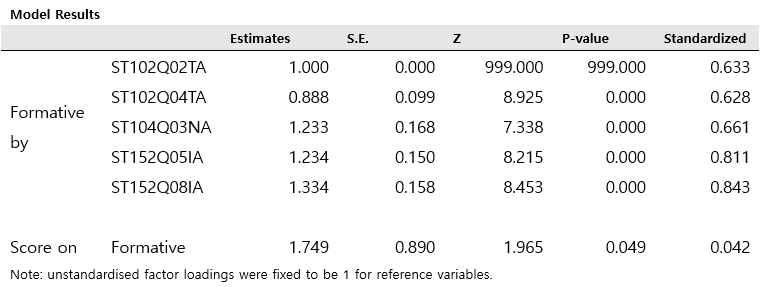
Model fits the data since χ2 statistic does not reject the null hypothesis. Also, other model fit indices, i.e., RMSEA, CFI, and SRMR, satisfies the rule of thumb. The effect of “Formative Assessment” on “Test Score” is statistically significant with regression coefficient 1.749 with standard error 0.890.
3.2. Mediation Analysis
- Factor Loadings
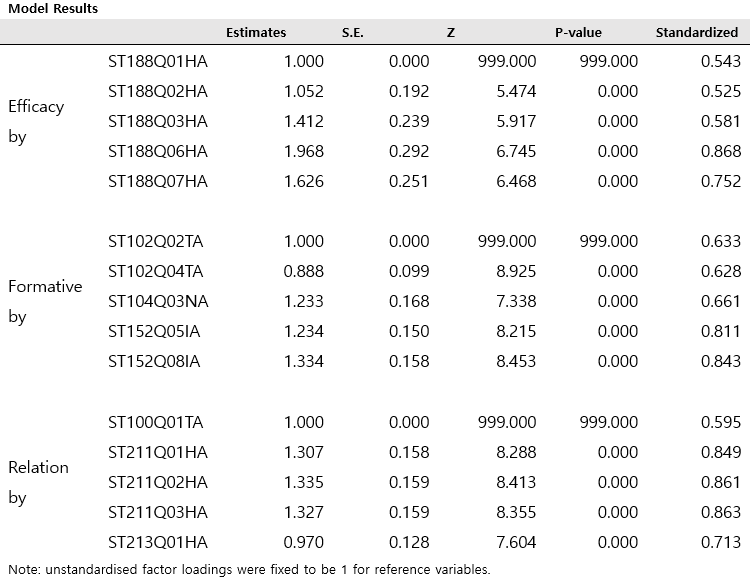
- Model Coefficients

When Mediators “Teacher-Student Relationship” and “Self-Efficacy” are add in the model, both direct effect and indirect effect became non-significant; coefficient from “Formative Assessment” to “Test Score” being 0.922 with standard error 0.946, and Sobel test statistic for indirect effect being 0.0768513.
- Model Fit Indices

Since some correlation between indicators from different factors were not fully explained by measurement model, the model fit was poor;χ2 value being 263.116 with p-value ≯ 0.05, RMSEA 0.096 ≮ 0.08, CFI 0.879 ≯ 0.95, and SRMR 0.093 ≮ 0.08.
- Mediation Model Diagram
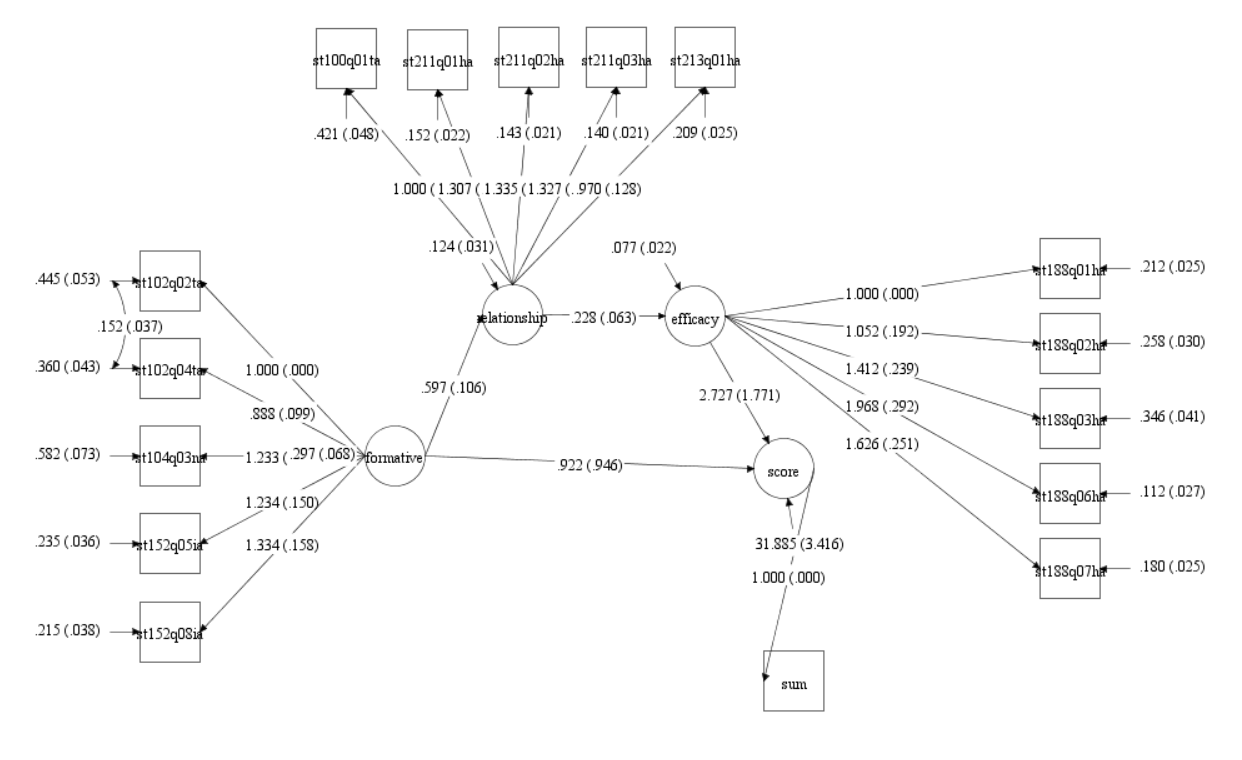
4. Discussion
In the analysis which has proceeded without mediators, although it was statistically significant, the effect of “Formative Assessment” on “Test Score” was weak. This result reinforces existing studies that formative assessment is not powerful itself to affect on mathematical performance(Pinger et.al., 2018), rather it is effective in assistance of cognitive activation(Yi & Lee, 2017).
In mediation analysis, direct effect of “Formative Assessment” on “Test Score” was 0.922 with standard error 0.946, and indirect effect of “Formative Assessment” on “Test Score” was 0.3711883. This results TheMediationProportion=IndirectEffectTotalEffect=0.2818035
5. Limitations and Future Directions
Since the effect of Formative Assessment on students’ math performance, further studies are required. Effects of formative assessment on test score in other test subjects need to be compared with this study in order to draw meaningful conclusion. In addition, efforts for discovering some mediators or latent variables which account for test score in Mathematics needs to be proceeded. Lastly, it needs to be investigated whether there is interaction between students’ academic competency and formative assessment on test score, which can be found in longitudinal studies.
Reference
Black, P., & Wiliam, D. (2005). Inside the black box: Raising standards through classroom assessment. Granada Learning.
Boston, C. (2002). The concept of formative assessment. Practical Assessment, Research, and Evaluation, 8(1), 9.
Fast L. A., Lewis J. L., Bryant M. J., Bocian K. A., Cardullo R. A., Rettig M., & Hammond K. A. (2010). Does math self-efficacy mediate the effect of the perceived classroom environment on standardized math test performance?. Journal of Educational Psychology. 102(3). 729-740.
Hughes, J. N., & Chen, Q. (2011). Reciprocal effects of student–teacher and student–peer relatedness: Effects on academic self efficacy. Journal of applied developmental psychology, 32(5), 278-287.
Pajares, F., & Graham, L. (1999). Self-efficacy, motivation constructs, and mathematics performance of entering middle school students. Contemporary educational psychology, 24(2), 124-139.
Pinger P., Rakoczy K., Besser M., & Klieme E.. (2018). Implementation of formative assessment – effects of quality of programme delivery on students’ mathematics achievement and interest. Assessment in Education: Principles, Policy & Practice. 25(2). 160-182.
PISA (2020, June, 20). What is PISA?. https://www.oecd.org/pisa/
Shepard, L. A. (2005). Linking formative assessment to scaffolding. Educational leadership, 63(3), 66-70.
Yi H. S., & Lee Y. (2017). A latent profile analysis and structural equation modeling of the instructional quality of mathematics classrooms based on the PISA 2012 results of Korea and Singapore. Asia Pacific Education Review. 18(1). 23-39.